I read about Norway’s remarkable dominance of the winter Olympics, despite its rather small population, and it piqued my interest:
With only five million people, it has won 303 winter Olympic medals, far more than any other country on the planet. To find a country smaller than world-leading Norway…, you have to travel down to Croatia, which ranks 24th with 11 medals. How Norway Scores So Much Olympic Gold, Wall Street Journal
I love this juxtaposition of unexpected data! Let’s turn it into a math project.
Four Math Project Requirements
As I’ve written before, when building a math project, I try to consider these four items, it always pushes the project from good to great:
- Authentic Data
- Intriguing Conflict Within The Data
- An Expert’s Perspective
- A Creative Product, Based On The Expert
The Wall Street Journal article provided a great start for the intriguing conflict:
- Can we rank Olympic performance not just by medals, but by medals compared to a country’s size?
- How do we measure size? Area or population? Is it significantly different?
- How do countries vary by summer and winter performance?
- What if we compare medals to other data, like gross domestic product, human development index, or the age of each country? Do any of these factors tie into Olympic performance?
Authentic Data
Of course, the internet has us covered for all of this data:
- Wikipedia has an awesome all-time Olympic Medal table, sortable by summer, winter, and total medals.
- Here’s a table ranking countries by population or countries by area
- Want to try gross domestic product or human development index? Do countries with stronger economies perform better in the Olympics?
Curriculum Connections
Use this data in any way that fits your students’ needs. Possibilities include:
Young students can:
- work with large numbers, ordering, adding, or subtracting.
- create simple bar graphs.
Older students can:
- dig into ratios
- graph scatter plots
- tackle issues of scale and outliers
And everyone should be analyzing the data they generate to look for patterns. Kids should form generalizations about size vs medal count, summer vs winter performance, medals vs economics, etc.
A bonus application for all ages is to use a spreadsheet to track data, make calculations, and create graphs. Doing this takes the emphasis away from repetitive calculations (which can become tedious) and places it on analysis (which is creative and exciting).
Expert Perspective
We’re really working with pure statistics here, so perhaps our students take on the role of a statistician, looking for hidden patterns underneath the data. A natural technique for this expert is to take raw data and graph it, visually spotting interesting trends.
The product can be as simple as a series of graphs, either on graph paper or created in a spreadsheet. And, of course, we’d want to see some written analysis: “What hidden patterns did you uncover?”
Graphing Samples
Here are a few sample graphs I made to whet your appetite.
Total Medals vs Population
| Country Name | Total Medals | Population (millions) |
|---|---|---|
| Great Britain | 802 | 63 |
| France | 765 | 66 |
| Norway | 451 | 5 |
| Japan | 435 | 127 |
| Canada | 423 | 35 |
| South Korea | 288 | 50 |
| Austria | 287 | 9 |
| Brazil | 108 | 220 |
| New Zealand | 100 | 5 |
This scatterplot compares total Olympic medals vs population in millions using nine countries.

The fun part is analyzing the results. By graphing the information, we get some cool patterns that would otherwise have been invisible. For example:
- France and Great Britain are not only physical neighbors, but are medal neighbors as well.
- South Korea/Austria and Canada/Norway pair up nicely also, despite being physically quite distant.
- Brazil and New Zealand are population outliers, but have nearly identical medal counts.
- New Zealand, Austria, and Norway are similar in population, but their medal counts jump significantly.
- Japan strikes a near perfect balance of large populations and medal counts.
Winter vs. Summer
| Country Name | Winter Medals | Summer Medals |
|---|---|---|
| Great Britain | 22 | 780 |
| France | 94 | 671 |
| Japan | 37 | 398 |
| Canada | 145 | 278 |
| South Korea | 45 | 243 |
| Norway | 303 | 148 |
| Brazil | 0 | 108 |
| New Zealand | 1 | 99 |
| Austria | 201 | 86 |
I also graphed summer vs winter totals and overlaid a rough “temperature gradient” to show each country’s seasonal dominance:

Some analysis:
- Canada is the closest to a perfect balance between summer and winter.
- Great Britain and France favor the summer
- Norway and Austria are strong in winter, but weak in summer.
- Brazil and New Zealand share an almost identical ratio.
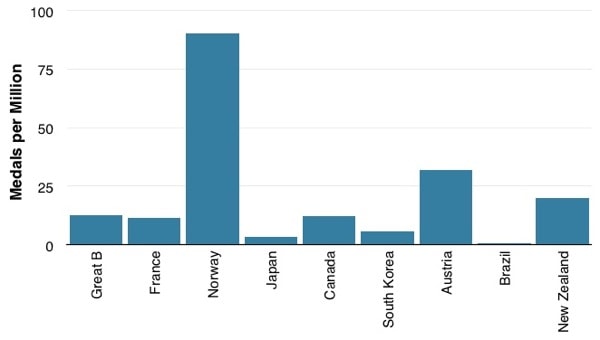
Ratios
If your students are older, have them calculate ratios. Perhaps total medals per million people?
| Country Name | Ratio (medals per million) |
|---|---|
| Great Britain | 12.8 |
| France | 11.6 |
| Norway | 90.2 |
| Japan | 3.4 |
| Canada | 12.1 |
| South Korea | 5.8 |
| Austria | 31.9 |
| Brazil | 0.5 |
| New Zealand | 20.0 |
- Norway may only have 5 millions citizens, but with 451 medals, each million people get to share 90 medals!
- Because of a large population and small medal count, Brazil’s citizens only get half a medal per million people.
- Great Britain, France, and Canada have remarkably similar ratios of ~12 medals per million.
- New Zealand may only have 100 medals total, but with a small population, each million get 20 medals.
And of course there’s no reason not to graph these ratios as well!
On Choosing Countries
It’s fun to let kids select their own countries to analyze (probably no more than ten), but beware of countries like the US, China, or India whose medal counts or populations absolutely destroy the graphs’ scales. Unless, of course, that’s the point of the lesson (perhaps you’re teaching logarithmic scales?).
Please let me know what you do with this and what your students come up with!
